Архимед (287 до н. э. — 212 до н. э.) родился в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку.
После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. В теоретическом отношении труд этого великого ученого был блистателен. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В сочинении «Параболы квадратуры» Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде «Об измерении круга» Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга. Мы до сих пор пользуемся придуманной Архимедом системой наименования целых чисел. Любопытен отзыв Цицерона, великого оратора древности, увидевшего «архимедову сферу» — модель, показывающую движение небесных светил вокруг Земли: «Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть».
Архимед проверяет и создает теорию пяти механизмов, известных в его время и именуемых «простые механизмы». Это — рычаг («Дайте мне точку опоры, — говорил Архимед, — и я сдвину Землю»), клин, блок, бесконечный винт и лебедка.
Но Архимед знал также, что предметы имеют не только форму и измерение: они движутся, или могут двигаться, или остаются неподвижными под действием определенных сил, которые двигают предметы вперед или приводят в равновесие. Великий сиракузец изучал эти силы и изобретал новую отрасль математики, в которой материальные тела, приведенные к их геометрической форме, сохраняют в то же время свою тяжесть. Эта геометрия веса и есть рациональная механика, статика, а также гидростатика.
Учение о гидростатике Архимед развивает в труде «О плавающих телах». «Предположим, — говорит ученый, — что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается еще чем-нибудь другим». Полагаясь на это положение, Архимед математически доказывает, что следующие ниже «следствия» полностью объясняются с помощью приведенной гипотезы:
- Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз.
- Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости.
- Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной (части тела), имел вес, равный весу всего тела.
- Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела.
- Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
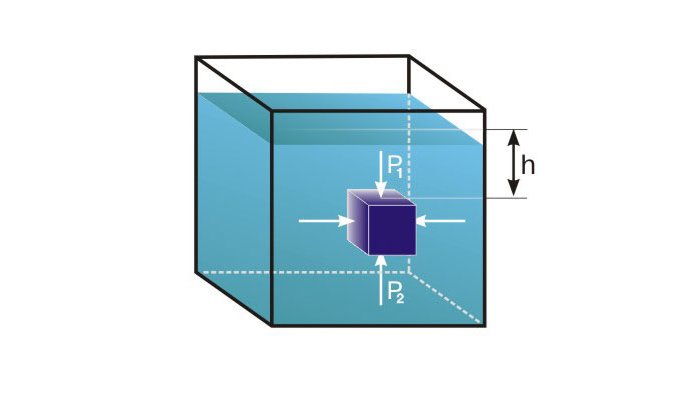
Пункт 5 содержит фактически общеизвестный закон Архимеда, открытие которого позволило ему, согласно преданию, осуществить проверку состава короны сиракузского царя Гиерона. Знаменитый рассказ о первом практическом применении Закона Архимеда приведен у древнеримского автора Витрувия в его труде «Об архитектуре»:
«…Исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, — один из золота, другой из серебра. Сделав это, он наполнил водой сосуд до самых краев и опустил в него серебряный слиток, и вот, какой объем слитка был погружен в сосуд, соответственное ему количество вытекло воды. Вынув слиток, он долил в сосуд такое количество воды, на какое количество стало там ее меньше, отмеряя вливаемую воду секстарием, чтобы, как и прежде, сосуд был наполнен водой до самых краев. Так отсюда он нашел, какой вес серебра соответствует какому определенному количеству воды.
Произведя такое исследование, он после этого таким же образом опустил золотой слиток в полный сосуд. Потом, вынув его и добавив той же мерой вылившееся количество воды, нашел на основании меньшего количества секстариев воды, насколько меньший объем занимает слиток золота по сравнению с одинаково с ним весящим слитком серебра. После этого, наполнив сосуд и опустив в ту же воду корону, нашел, что при погружении короны вытекло больше воды, чем при погружении золотой массы одинакового с ней веса; и таким образом на основании того заключения, что короной вытеснялось большее количество воды, чем золотым слитком, он вскрыл примесь в золоте серебра и обнаружил явное воровство поставщика».
«В этом рассказе, — отмечает Я.Г. Дорфман, — убедительно лишь заключение Архимеда о том, что корона состоит из сплава, а не из чистого золота. Но ниоткуда не следует, что второй компонентой было обязательно серебро. Во всяком случае, следует отметить, что это выдающееся открытие Архимеда знаменует собой первое в истории применение физического измерительного метода к контролю и анализу химического состава без нарушения целостности изделия. Огромное практическое значение этого открытия в эпоху, когда еще никаких других методов подобного рода не было, естественно, привлекло к себе всеобщее внимание и стало предметом дальнейших исследований и практических использований на протяжении многих последующих веков.
По-видимому, и сам Архимед не ограничился описанным полукачественным экспериментом, а перешел к более точному количественному измерению. Автор арабского сочинения XII века „Книга о весах мудрости“ ал-Хазини, цитируя „слово в слово“ не дошедший до нас трактат грека Менелая, жившего во времена римского императора Домициана (81–96 гг. до н. э.), сообщает, что Архимед „изобрел механическое приспособление, которое благодаря своему тонкому устройству позволило ему определить, сколько золота и сколько серебра содержится в короне, не нарушая ее формы“. Ал-Хазини приводит также схему устройства „весов Архимеда“ с подвижным грузом. Сравнивая на этом приборе веса упомянутых слитков в воде, Архимед мог с помощью подвижного груза определять численное отношение удельных весов золота и серебра, а, сопоставляя таким же способом веса короны и одного из этих слитков, мог установить относительное количество золота и серебра в короне (если в состав короны входили только эти два металла)».
Синезий из Кирэны в IV веке, ученик знаменитой александрийской ученой Ипатии, основываясь на принципах Архимеда, изобрел «гидроскоп» — ареометр для определения удельного веса жидкостей. Прибор, изготовленный из бронзы, имел насечки. По-видимому, этот прибор использовался для составления таблиц удельных весов различных жидкостей. К сожалению, подобные таблицы до нас не дошли.
Из книги "Сто великих научных открытий"